Autor:Codenga27.11.2024

Exploratory Data Analysis – What Is It?

Data analysis is a critical process that helps us understand what our data contains, its characteristics, and how it behaves. The first step in this process is Exploratory Data Analysis (EDA). This stage allows us to preliminarily examine and summarize data before moving on to more advanced methods. EDA helps us better comprehend the dataset and draw initial insights from it.

How Does Exploratory Data Analysis Work?

EDA relies on descriptive statistics, simple tools designed to help us understand the distribution, structure, and main features of data. It’s important to note that descriptive statistics describe and summarize data but are not used to make inferences about the entire population. For this purpose, more advanced methods, such as inferential statistics, are employed.

Descriptive Statistics – Key Measures

Descriptive statistics provide insights into the distribution and behavior of data in a dataset. Below are the main categories and measures used:

1. Frequency Measures

These describe how often different values appear in a dataset, e.g., the number of times a specific value occurs.

2. Measures of Central Tendency

These measures help determine the "center" of the data:

• Arithmetic Mean – The sum of all values divided by the number of values.
• Median – The middle value in an ordered dataset.
• Mode – The most frequently occurring value in a dataset.

3. Measures of Dispersion

These reveal how varied the data is:

• Variance and Standard Deviation – Indicate how far data points deviate from the mean.
• Range – The difference between the highest and lowest values.

4. Skewness and Kurtosis

In addition to basic measures, the distribution’s characteristics, such as skewness and kurtosis, are also significant.

Measures of Skewness

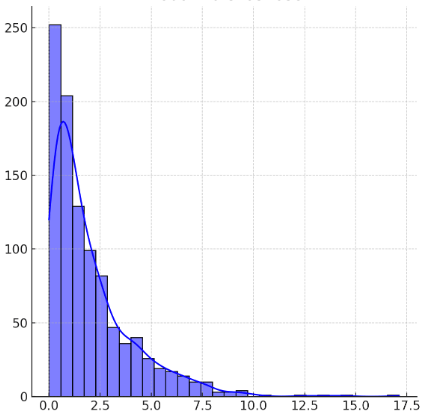
Right-skewed distribution – The tail of the distribution extends to the right, meaning most data is on the left.

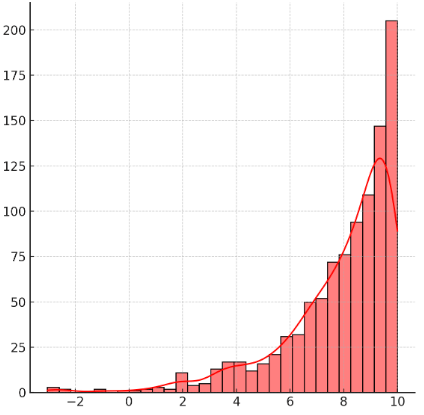
Left-skewed distribution – The tail extends to the left, meaning most data is on the right.

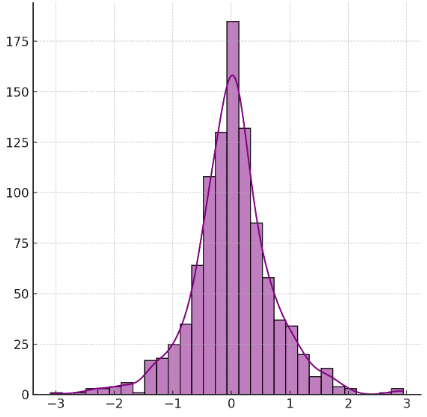
Kurtosis

High kurtosis – Data is heavily concentrated around the mean, resulting in a sharp peak.

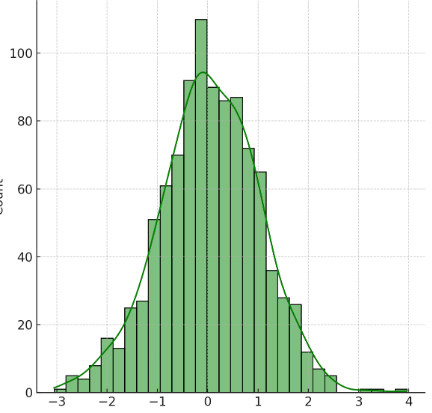
Low kurtosis – Data is more evenly spread, producing a flatter distribution.

Why Is Exploratory Data Analysis Important?

EDA is a crucial step in any analysis, as it helps to:

• Detect potential errors or inconsistencies in the data.
• Gain a better understanding of the data’s structure and characteristics.
• Prepare the data for more advanced analyses.

By conducting exploratory data analysis, we can consciously select appropriate analytical methods and tools to draw more accurate and precise conclusions.

Conclusion

Data exploration is the foundation of any analysis – the more we learn at this stage, the better equipped we are to address complex problems in later stages of the process.