Autor: Codenga 27.10.2023

In this article, we will explain what combinations and permutations are. These two concepts are an important part of the field known as combinatorics. We will explain each of these concepts using simple language and provide several examples. This article is intended for readers who have not previously encountered this topic and want to understand the meaning of combinations and permutations. To understand the content discussed in this article, the ability to calculate factorials is required.

Combinations - What Are They?

Combination is a concept in combinatorics that describes different sets of elements selected from a given set, but without considering the order in which these elements are arranged.

Here is the mathematical formula for combinations:

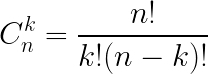
Where:

• n is the number of available elements.
• k is the number of positions or slots for placing the elements.

Example

If we have a set {A, B, C, D} and want to create a 2-element combination, we can do it in several ways:

• AB
• AC
• AD
• BC
• BD
• CD

All these combinations do not consider the order of elements and are simply different sets of selected elements from the set.

Let's make sure that we can indeed obtain 6 combinations of pairs from a 4-element set. To do this, we will use the formula shown earlier.

The set has 4 elements (n = 4). We want to generate 2-element combinations, so k = 2. Let's plug our data into the formula:

n! / (k!(n-k)!) = 4! / (2!(4 - 2)! = 24 / (2 * 2!) = 24 / (2 * 2) = 24 / 4 = 6

Everything checks out. Our predictions have been confirmed by calculations. So, the basic concept of combinations is nothing more than a certain set of elements from a set, without considering the order of elements (in other words, the positions of elements do not matter).

Permutations - What Are They?

Permutation is a concept in mathematics and combinatorics that describes different ways of arranging or ordering elements in a specific sequence. You can think of it as different arrangements or orders in which you can place given elements.

Example

Suppose we have three different billiard balls labeled A, B, and C. Permuting these elements means finding different ways to arrange the elements A, B, and C. Here are some examples of permutations of our billiard balls:

• ABC
• ACB
• BAC
• BCA
• CAB
• CBA

We can arrange our 3 balls in 6 different configurations. How do we know that we can arrange them in a maximum of 6 ways? In this case, the factorial comes in handy.

Simply calculate the factorial of all the elements in the set (we have 3 elements: A, B, and C), which is 3! = 3 * 2 * 1 = 6 (3 balls can be arranged in 6 different ways).

Here's a very simple rule - want to know how many possible permutations there are in a given set? Just calculate the factorial of all the elements in the set.

Summary and Next Steps

We hope that after reading this article, you now understand what combinations and permutations are. They are a very important part of the field known as combinatorics.